并发编程网 - ifeve.com

原文链接  译者: 李璟(jlee381344197@gmail.com)

这是一块非常简单的Java代码片段：

[code lang=”java”]
public class HelloWorld{

public static void main(String []args){

int product = 1;

for (int i = 10; i <= 99; i++) {

product *= i;

}

System.out.println(product);

}

}
[/code]

为什么得出的结果是0呢？

问题现象

蛋疼的同学可能会发现这个程序执行的规律：
1 * 10 = 10

10 * 11 = 110

110 * 12 = 1320

1320 * 13 = 17160

17160 * 14 = 240240

240240 * 15 = 3603600

3603600 * 16 = 57657600

57657600 * 17 = 980179200

……

 

-1342177280 * 40 = -2147483648

-2147483648 * 41 = -2147483648

-2147483648 * 42 = 0

0 * 43 = 0

0 * 44 = 0

……

0 * 97 = 0

0 * 98 = 0
程序从42开始就已经输出0，所以42以后的数字相乘的结果就显而易见了。从结果中发现，乘积的符号已一种难以理解的方式变换着，表明乘积已经溢出了，同时也说明Java并不会理会整数的上下溢出。

问题解答

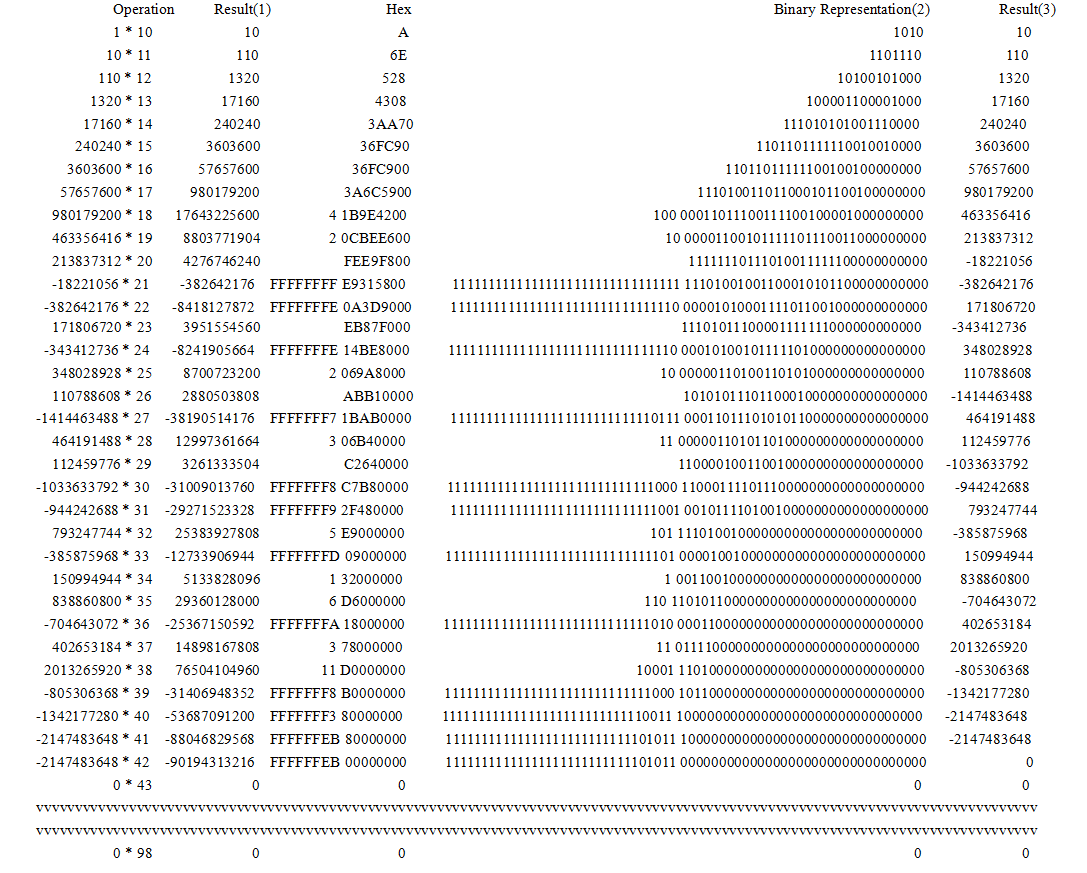
请记住Java的int类型是32位的有符号二进制补码表示的数字类型(译者注：64为jdk同样如此)。这是每一步乘法在计算机内部所做的操作：

标注(1)是实际十进制结果。

标注(2)十六进制以及十进制的内部表示结果，int类型只会存储低32位的数据。

标注(3)是标注(2)的补码形式。

如果你好奇0从哪里来，请仔细看上方2进制表示的结果。细心的同学会注意到：

任何一个数与偶数相乘得偶数。

偶数与偶数相乘，会将2进制位整体左移，0从右边填补空位。

偶数与奇数相乘，不会改变最右方0的数量。

当乘法执行的足够多次时，右方的0位会越来越多。最终，连续乘到42时，乘积的2进制表示的低32位全是0，所以int将会是0。

问题扩展

既然知道了问题的原因，我们换一种变量来做同样的操作，以byte为例。

Java的byte变量是8位的有符号数，同样也是补码表示。从上方结果表格看出，连续从10乘到16时，2进制结果的低8位全都是0，所以此时的byte变量是0。而连续乘到15时，低8位是10010000，还记得怎么由补码求原码吗？很简单， 符号位不变，其余位取反加1，得出11110000，既-112，感兴趣的朋友请在自己机器上验证结果。